|
|
|
| Diktat Logika Matematika | ||
| Sebelum Ini | Fungsi Boolean | Setelah Ini |
| Daftar Isi | |||||||
| II.1 | Rangkaian Saklar
|
||||||
| II.2 | Gerbang Logika
|
||||||
| II.3 | Fungsi Boolean dan Rangkaian Kombinatorial
|
||||||
Sebelum kita melihat definisi fungsi boolean, kita bahas dulu rangkaian saklar. Saklar merupakan piranti
listrik yang diasumsikan memiliki 2 kondisi On atau Off . Perhatikan rangkaian listrik
pada gambar 2.1
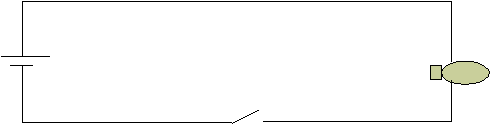
Gambar 2.1 Rangkaian Saklar
Rangkain saklar memiliki 2 objek yaitu saklar dan lampu. Saklar dapat dianggap sebagai masukan dan
memiliki 2 keadaan yaitu On dan Off. Lampu sebagai keluaran memiliki keadaan tergantung dengan keadaan
saklar. Apabila saklar On maka lampu akan On, apabila saklar Off maka lampu Off. Tabel 2.1 menunjukkan keadaan
rangkaian saklar dan lampu.
| Saklar | Lampu |
|---|---|
| On | On |
| Off | Off |
2 Saklar dapat dirangkai secara paralel seperti pada gambar 2.2.
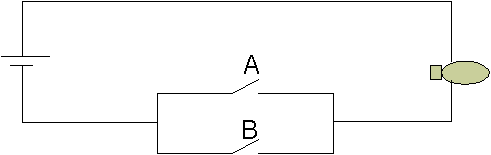
Gambar 2.2 Rangkaian Saklar Paralel
Lampu menyala apabila rangkaian membentuk rangkaian tertutup atau dalam kata lain
ada arus yang mengalir ke lampu. Jika kita selidiki semua keadaan saklar pada rangkaian paralel (gambar 2.2)
maka kita akan memperoleh tabel 2.2
| Saklar A | Saklar B | Lampu |
|---|---|---|
| On | On | On |
| On | Off | On |
| Off | On | On |
| Off | Off | Off |
2 Saklar dapat dirangkai secara seri seperti pada gambar 2.3
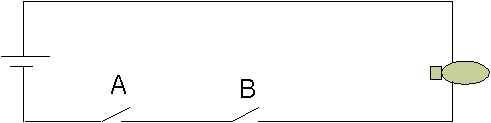
Gambar 2.3 Rangkaian Saklar Seri
Jika kita selidiki semua keadaan saklar pada rangkaian seri (gambar 2.2)
maka kita akan memperoleh tabel 2.4
| Saklar A | Saklar B | Lampu |
|---|---|---|
| On | On | On |
| On | Off | Off |
| Off | On | Off |
| Off | Off | Off |
Apabila terdapat 3 atau lebih saklar, kita dapat merangkai saklar tersebut secara kombinasi seri dan paralel. Keadaan Output (lampu) tergantung dengan bagaimana saklar-saklar tersebut dirangkai. Contoh apabila terdapat 3 saklar sebut A,B dan C maka kita dapat menrangkai B dan C secara seri baru kemudia Paralel dengan A seperti pada gambar 2.4
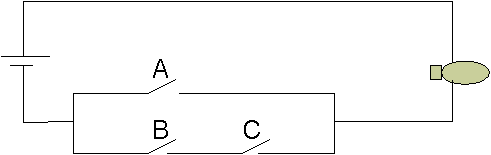
Gambar 2.4 Rangkaian Kombinatorial Saklar
Tabel keadaan dan Output rangkaian pada gambar 2.4 diberikan oleh tabel 2.4
| Saklar A | Saklar B | Saklar C | Lampu |
|---|---|---|---|
| On | On | On | On |
| On | On | Off | On |
| On | Off | On | On |
| On | Off | Off | On |
| Off | On | On | On |
| Off | On | Off | Off |
| Off | Off | On | Off |
| Off | Off | Off | Off |
Rangkaian pada gambar 2.4 dapat direpresentasikan dengan ekpressi boolean
Lampu = A + (B.C) dengan A,B dan C merepresentasikan saklar A, saklar B dan Saklar C
Representasi rangkaian listrik dengan saklar pada bagian sebelumnya ternyata tidak praktis untuk'
pembuatan rangkaian logika karena tidak secara langsung mendefinisikan operator boolean.
Dalam praktiknya operator-operator boolean dapat direpresentasikan oleh suatu gerbang yang disebut
gerbang logika.
Gerbang logika merupakan suatu gerbang yang memiliki input dan output. Baik input ataupun output
hanya dapat bernilai satu dari 2 kemungkinan yaitu high atau low.
Dalam implementasinya high dan low adalah tegangan listrik dan merupakan konsep digital.
Nilai high direpresentasikan oleh simbol 1, dan nilai low direpresentasikan oleh simbol 0.
Seperti yang telah kita pelajari, aljabar boolean memiliki 3 operator dasar jadi terdapat 3
gerbang dasar.
Berikut ini kita akan mempelajari konvesi gambar gerbang-gerbang dasar tersebut.
Gerbang OR direpresentasikan oleh gambar 2.5
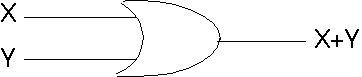
Gambar 2.5 Gerbang OR
Tabel kebenaran gerbang OR diberikan oleh tabel 2.5 (Catatan : Output dilambangkan dengan X+Y)
| X | Y | X+Y |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Gerbang AND direpresentasikan oleh gambar 2.6

Gambar 2.6 Gerbang AND
Tabel kebenaran gerbang AND diberikan oleh tabel 2.6 (Catatan : Output dilambangkan dengan X.Y)
| X | Y | X.Y |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
Gerbang NOT direpresentasikan oleh gambar 2.7
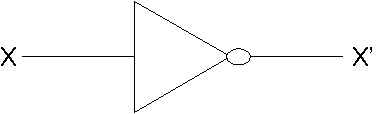
Gambar 2.7 Gerbang NOT
Tabel kebenaran gerbang AND diberikan oleh tabel 2.6 (Catatan : Output dilambangkan dengan X')
| X | X' |
|---|---|
| 1 | 0 |
| 0 | 1 |
Fungsi boolean adalah pemetaan dari beberapa pasangan {0,1} ke {0,1}.
Fungsi boolean dibentuk oleh ekspressi boolean. Ekspressi boolean dibentuk oleh variabel-variabel boolean
yang direpresentasikan oleh huruf besar A,B,C,...,Z dan operator-operator boolean + (or) ,. (and),
dan ' (komplemen).
Kita juga menggunakan (,) dan = sebagai simbol bantu.
Fungsi boolean dilambangkan dengan f(X,Y,..)
X,Y,... adalah variabel bebas yang dapat bernilai 1 atau 0 dan f adalah nama fungsi.
Contoh :
f(X,Y) = (X+Y)' [1]
Fungsi [1] apabila variabel X dan Y diberi nilai berturut-turut 0 dan 1 maka bernilai
f(0,1) = (0+1)' = (1)'= 1'= 0
Kita dapat menganalisa semua kemungkinan nilai X dan Y dalam suatu tabel yang disebut tabel kebenaran.
| X | Y | (X+Y)' |
|---|---|---|
| 1 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
Setiap fungsi boolean dapat direpresentasikan oleh rangkaian kombinatorial gerbang logika.
Caranya adalah dengan merepresentaasikan tiap operator pada fungsi dengan gerbang yang berhubungan lalu
lalu output dari suatu ekpresi dasar menjadi input gerbang yang merepresentasikan operator yang presedensnya lebih rendah.
Contoh
f(X,Y) = (X+Y)' dapat direpresentasikan oleh rangkaian kombinatorial pada gambar 2.8
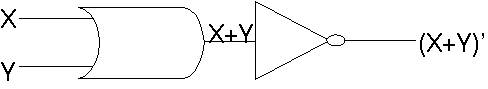
Gambar 2.8 Rankaian Kombinatorial f(X,Y) = (X+Y)'
Kita dapat membentuk rangkaian yang lebih rumit lagi dengan menggunakan lebih banyak gerbang, contoh seperti pada gambar 2.9.
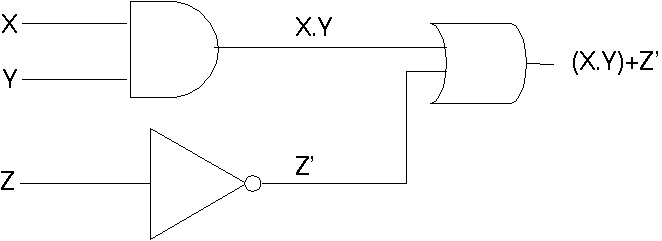
Gambar 2.9 Rankaian Kombinatorial f(X,Y,Z) = (X.Y)+Z'
Tabel kebenaran f(X,Y,Z) = (X.Y)+Z' diberikan oleh tabel 2.8
| X | Y | Z | X.Y | Z' | X.Y + Z' |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | 1 |
| Sebelum Ini | Daftar Isi | Setelah Ini |
| Sistem Boolean | Simplifikasi Fungsi Boolean |