|
|
|
| Diktat Logika Matematika | ||
| Sebelum Ini | Sistem Boolean | Setelah Ini |
| Daftar Isi | |
| I.1 | Himpunan |
| I.2 | Operator Boolean |
| I.3 | Simbol 1 dan 0 |
| I.4 | Aljabar Boolean |
| I.5 | Hukum Aljabar Boolean |
| I.6 | Hukum Turunan Aljabar Boolean |
| I.7 | Sifat Dual Aljabar Boolean |
| I.8 | Aljabar Boolean Untuk 1 dan 0 |
Sistem boolean bersandar pada teori himpunan.
Himpunan adalah kumpulan objek. Objek dapat berupa apa saja.
Misalnya A adalah sebuah himpunan yang memiliki anggota (disebut elemen)
bilangan prima yang lebih kecil daripada 10
A = {2,3,5,7}
Notasi { dan } digunakan untuk menandakan himpunan.
Contoh :
B adalah himpunan dengan anggotanya adalah bilangan ganjil lebih kecil daripada 10 maka
B = {1,3,5,7,9}
Himpunan yang dipakai dalam sistem boolean adalah himpunan crisp. Yang artinya apabila terdapat objek x dan himpunan A maka x dapat dinyatakan sebagai (pilih salah satu) anggota himpunan A atau bukan anggota himpunan A
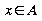 atau
atau 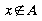
Kita tidak akan membahas himpunan lebih jauh, anda akan mendapatkan topik ini lebih dalam pada mata kuliah matematika diskrit
[Kembali ke Atas]
3 Operator dikenal di sistem Boolean. Yaitu
| No | Operator | Keterangan |
|---|---|---|
| 1 | + (baca : tambah logika) | Operator + merupakan operator binary (membutuhkan 2 operand). Apabila A dan B adalah himpunan maka A+B adalah himpunan dengan elemen merupakan elemen A atau elemen B Dalam kata lain, A + B ekivalen dengan A union B |
| 2 | . (baca : perkalian logika) | Operator . merupakan operator binary (membutuhkan 2 operand). Apabila A dan B adalah himpunan maka A.B adalah himpunan dengan elemen merupakan elemen A dan elemen B Dalam kata lain, A.B ekivalen dengan A intersects B |
| 3 | ' (baca : komplemen) | Operator ' merupakan operator unary (membutuhkan 1 operand). Apabila S adalah himpunan semesta maka A' adalah himpunan dengan elemen merupakan bukan elemen A |
Selain 3 operator, sistem boolean menggunakan simbol 1 dan 0.
1 melambangkan himpunan semesta. Himpunan semesta dapat dianggap sebagai himpunan dengan anggota
segala sesuatu. Namun, dalam prakteknya semesta selalu dianggap sebagai semesta kecil (himpunan bagian
dari semesta).
0 melambangkan ketiadaan atau himpunan kosong.
Contoh :
Misalnya Semesta adalah bilangan asli dari 1 sampai dengan 10 atau
S = {1,2,3,4,5,6,7,8,9,10}
Didefinisikan A adalah himpunan bilangan ganjil pada semesta S
A = {1,3,5,7,9}
B adalah himpunan bilangan genap pada semesta S
B = {2,4,6,8,10}
dan C adalah himpunan bilangan prima pada semesta S
C = {2,3,5,7}
maka
A+B = {1,2,3,4,5,6,7,8,9,10} = 1
A+C = {1,2,3,5,7,9}
A.B = {} = 0
A.C = {3,5,7}
C' = {1,4,6,8,9,10}
Sesuatu A disebut aljabar boolean sebagai himpunan yang terdiri dari
S (Semesta), operator +,. dan ' serta simbol 1 dan 0.
Atau sering dilambangkan
A = < S.+,.,',1,0 >
Aljabar boolean juga menggunakan simbol tambahan yaitu (,) dan =.
( dan ) digunakan untuk membuat presedens tertinggi.Sedangkan, '=' digunakan untuk penugasan nilai.
Hukum-hukum berikut ini merupakan aksioma di dalam aljabar boolean (sesuatu yang benar tanpa bukti).
| Hukum | Arti |
|---|---|
| Komutatif |
A + B = B + A A.B = B.A |
| Assosiatif |
A + (B + C) = (A + B) + C (A.B).C = A.(B.C) |
| Distributif |
A + (B.C) = (A+B).(A+C) A.(B+C) = (A.B) + (A.C) |
| Identitas |
A.1 = A A + 0 = A |
| Komplemen |
A + A' = 1 A.A' = 0 |
Hukum-hukum berikut ini merupakan hukum hasil turunan aksioma di dalam aljabar boolean (bukti diturunkan dari aksioma).
| Hukum | Arti |
|---|---|
| Idempotensi |
A + A +... + A = A A.A. ... .A = A |
| Involusi | (A')' = A |
| Perkalian 0 / Pertambahan 1 |
A.0 = 0 A + 1 = 1 |
| Komplemen 1 dan 0 |
1' = 0 0' = 1 |
| Peleburan |
X + XY = X X . (X+Y) = X |
| De Morgan |
( X + Y )' = X'.Y' (X .Y)' = X' + Y' |
| A.1 = A | Hukum Identitas |
| A.(A+A') = A | Hukum Komplemen |
| (A.A) + (A.A') = A | Hukum Distributif |
| (A.A) + 0 = A | Hukum Komplemen |
| A.A = A | Hukum Identitas (Q.E.D) |
| X.1 + XY = X | Hukum Identitas |
| X.(1+Y) = X | Hukum Distribusi |
| X.1 = X | Hukum Pertambahan 1 |
| X = X | Hukum Identitas (Q.E,D) |
Perhatikan setiap hukum Aljabar Boolean selalu bersifat dual.
Artinya apabila suatu hukum berlaku terhadap operator +,. dan 1
maka hukum tersebut juga berlaku dengan mengubah operator
+ menjadi . dan sebaliknya . menjadi +
dan
1 menjadi 0 dan sebaliknya 0 menjadi 1
Langsung dari hukum-hukum aljabar, terdapat hukum-hukum turunan yang variabelnya bernilai 1 atau 0 seperti berikut ini :
1 + 1 = 1 (Idempotens)
1 + 0 = 1 (Identitas)
0 + 1 = 1 (Identitas + Komutatif)
0 + 0 = 0 (Idempotens / Identitas)
Untuk operator . diperoleh hukum-hukum
1 . 1 = 1 (Idempotens / Identitas)
1 . 0 = 0 (Hk Perkalian 0)
0 . 1 = 0 (Hk Perkalian 0)
0 . 0 = 0 (Idempotens)
| Sebelum Ini | Daftar Isi | Setelah Ini |
| Sillabus | Fungsi Boolean |