|
|
|
| Diktat Logika Matematika | ||
| Sebelum Ini | Interpretasi Logika Predikat | |
| Daftar Isi | |
| IX.1 | Motivasi |
| IX.2 | Interpretasi |
| IX.3 | Aturan Semantik |
| IX.4 | Interpretasi Termodifikasi |
| IX.5 | Aturan untuk Kuantifier |
| IX.6 | Latihan |
Interpretasi menugaskan makna untuk tiap simbol pada logika predikat yakni : konstan,
fungsi dan predikat. Interpretasi menugaskan suatu nilai pada domain atau disebut objek
kepada konstan dan variabel, fungsi atas domain kepada simbol fungsi dan relasi atas domain
pada simbol predikat.
Contoh : terdapat kalimat logika predikat tertutup seperti berikut
G : if (∀ x)(∃ y) p(x,y) then p(a,f(a))
Sembarang interpretasi atas G harus menentukan domain dan menugaskan nilai ke tiap simbol
dan terutama ke konstan a, fungsi f dan predikat p.
Misal sekarang terdapat interpretasi I dengan domain D adalah bilangan integer
dan diinterpretasikan untuk tiap simbol
f adalah fungsi suksessor yaitu fungsi f(d) adalah d + 1.
p adalah relasi lebih besar dari yaitu relasi p(d1,d2) adalah d1 > d2
Berdasarkan interpretasi I, maka kalimat G dapat ditentukan nilai kebenaranya.
Perhatikan sub kalimat p(a,f(a)) berdasarkan interpretasi I adalah pertidaksamaan
berikut
0 > 0 + 1
Oleh karena 0+1 adalah 1, dan karena 0 > 1 adalah bernilai false maka
predikat p(a,f(a)) dalam interpretasi I adalah bernilai false
Kalimat G dapat diketahui nilai kebenarannya apabila bagian anteseden diketahui yaitu kalimat :
(∀ x)(∃ y) p(x,y)
Berdasarkan interpretasi I anteseden itu dapat diterjemahkan menjadi :
Untuk semua integer d, terdapat integer d' sehingga d > d'
kalimat ini bernilai true (ambil d adalah d dan d' adalah d-1).
Karena bagian anteseden dan konsekwen kalimat G telah diketahui makna kebenarannya, kalimat
G dapat diketahui dengan aturan implikasi yaitu
if true then false 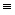 false
false
Definisi.
Didefinisikan D adalah himpunan elemen sembarang.
Sebuah interpretasi I atas domain D memberikan nilai ke tiap simbol
konstan, variabel, fungsi dan predikat sebagai berikut
Aturan semantik pada logika predikat mengadopsi semua aturan semantik pada logika proposisi dengan ditambah sebagai berikut :
Iterpretasi termodifikasi atas domain D untuk Interpretasi I untuk
sembarang variabel x ditulis sebagai :
< x <-- d > o I
adalah
Perhatikan kalimat logika predikat berikut ini
| (a) | p(a,x) |
| (b) | p(x,a) and p(x,f(x)) |
| (c) | (∃ y) p(y,x) |
| (d) | (∃ y) [ p(y,a) or p(f(y),y)] |
| (e) | (∀ x)(∃ y) p(x,y) |
| (f) | (∃ y)(∀ x) p(x,y) |
Berdasarkan interpretasi I maka kalimat tersebut dapat ditentukan nilai kebenarannya yaitu
| (a) |
p(a,x) dalam interpretasi I dapat digantikan dengan
kalimat biasa 0 < 1 Oleh karena 0 lebih kecil dari 1 adalah true maka Nilai p(a,x) pada interpretasi I adalah true |
| (b) |
p(x,a) and p(x,f(x)) dalam interpretasi I dapat digantikan dengan
kalimat biasa 1 < 0 and 1 < (1+1) 1 < 0 and 1 < 2 Oleh karena 1 tidak lebih kecil dari 0, maka p(x,a) bernilai false Oleh karena 1 lebih kecil dari 2, maka p(x,f(x)) bernilai true Sehingga kalimat (b) dapat diubah menjadi false and true yang ekivalen dengan false |
| (c) |
(∃ y) p(y,x) dalam interpretasi I dapat
diganti dengan kalimat biasa Ada integer y, sehingga y < 1 Berdasarkan aturan ∃ terdapat interpretasi termodifikasi sehingga y < 1 bernilai true, yaitu < y <-- 0 > o I sehingga (∃ y) (y < 1) bernilai true |
| (d) |
(∃ y) [ p(y,a) or p(f(y),y)] dalam interpretasi I
dapat diganti dengan kalimat biasa yaitu : Ada integer y sehingga (y < 0) atau ((y+1) < y) Berdasarkan aturan ∃, agar bernilai true harus ada bilangan d yang merupakan bilangan nonnegatif yang memenuhi interpretasi termodifikasi < y <-- d > o I Sehingga (d < 0) atau ((d+1) < d) bernilai true Untuk subkalimat pertama (d < 0) tidak ada bilangan d pada non negatif yang memenuhi (d < 0) sedangkan subkalimat kedua ((d+1) < d) tidak ada bilangan d pada non negatif yang memenuhi ((d+1) < d) Sehingga tidak ada bilangan d di integer non negatif yang memenuhi (d < 0) atau ((d+1) < d) Jadi, nilai (∃ y) [ p(y,a) or p(f(y),y)] dalam interpretasi I adalah bernilai false |
| (e) |
(∀ x)(∃ y) p(x,y) dalam interpretasi I dapat diterjemahkan menjadi kalimat biasa yaitu Untuk semua integer nonnegatif x terdapat integer nonnegatif y sehingga berlaku x < y Berdasarkan aturan ∀ nilai kalimat (e) bernilai true apabila untuk semua bilangan d1 di noninteger ada bilangan d2 di noniteger sehingga interpretasi termodifikasi < x <-- d1 > o < y <-- d2 > o I bernilai true Sekarang bila dimodifikasi d2 sebagai d1+1 maka kalimatnya menjadi untuk semua bilangan d1 di noninteger ada bilangan d1+1 sehingga (d1 < (d1+1)). Kalimat ada bilangan d1+1 sehingga (d1 < (d1+1)) bernilai true untuk semua bilangan d1 sehingga Kalimat (∀ x)(∃ y) p(x,y) bernilai true pada interpretasi I |
| (f) |
(∃ y)(∀ x) p(x,y) Dalam interpretasi I dapat dibaca sebagai Ada bilangan integer non negatif y sehingga Semua bilangan integer non negatif x berlaku (x < y ) Berdasarkan aturan ∃ kalimat (f) bernilai true apabila Terdapat bilangan d1 di integer nonnegatif dan Semua bilangan d2 di integer nonnegatif yang mengakibatkan interpretasi termodifikasi x <-- d2 dan y <-- d1 (d2 < d1 ) bernilai true. Perhatikan untuk semua d1 pada bilangan integer non negatif Apabila d2 = d1, maka (d2 < d1) benilai false maka kalimat (∃ y)(∀ x) p(x,y) dalam interpretasi I adalah bernilai false |
| Sebelum Ini | Daftar Isi | |
| Dasar Logika Predikat |