|
|
|
| Diktat Logika Matematika | ||
| Sebelum Ini | Dasar Logika Predikat | Setelah Ini |
| Daftar Isi | |||||||||||
| VIII.1 | Pendahuluan | ||||||||||
| VIII.2 | Sintaksis
|
||||||||||
| VIII.3 | Variabel Bebas dan Terikat (free and bound variables ) | ||||||||||
| VIII.4 | Soal Latihan | ||||||||||
Pada logika proposisional sebuah kalimat dapat ditentukan nilai kebenarannya
dengan hanya memperhatikan struktur kalimat tersebut. Seperti kalimat
| Kalimat 1 : |
Andi suka makan bakso atau Andi tidak suka makan bakso |
| P or (not P) |
Ada beberapa kalimat, sayangnya, tidak dapat dikatakan benar berdasarkan struktur
karena bukan perwujudan (Instance) dari sembarang kalimat valid logika proposisional.
Sebagai contoh, kalimat- kalimat
| Kalimat 2 : |
Ada manusia yang jujur di Indonesia atau Semua manusia di Indonesia tidak jujur |
|
| Kalimat 3 : |
Ada bilangan ganjil yang merupakan bilangan prima atau Semua bilangan prima bukan merupakan bilangan ganjil |
|
| F : |
( ∃ x)[p(x) and q(x) ] or ( ∀ x)[if p(x) then not q(x) ] |
|
Terdapat manusia x yang memenuhi x itu jujur dan x adalah orang Indonesia atau Untuk semua manusia x, jika x jujur maka x adalah bukan orang Indonesia. |
Bahasa logika predikat memiliki tata aturan. Sintaksis hanya membicarakan tata aturan pembentukan kalimat dalam logika predikat yang benar tanpa memperhatikan arti kalimat tersebut.
[Kembali ke Atas]Bahasa logika predikat menggunakan simbol-simbol yang merupakan unsur pembentuk kalimat logika predikat. Simbol-simbol itu adalah :
Secara intuiftif, simbol konstan dan simbol variabel mendenotasikan suatu objek sedangkan simbol fungsi dan simbol relasi mendenotasikan relasi dan fungsi antar objek.
Untuk membentuk kalimat logika predikat digunakan tiga tahap yaitu : pembentukan term, pembentukan proposisi dan akhirnya pembentukan kalimat
[Kembali ke Atas]terms pada logika predikat adalah ekspresi yang mendenotasikan objek. Terms dibangun dengan aturan berikut.
Proposisi pada logika predikat dimaksudkan untuk merepresentasikan
relasi antar objek. Proposisi dibentuk dengan aturan berikut :
Kalimat dalam logika predikat dibangun oleh proposisi dengan menggunakan aturan berikut seperti pada logika proposisional
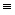 G)
G)
Setiap term yang dipakai untuk membangun term t (termasuk t) atau membangun sebuah kalimat
F disebut subterm dari t atau F.
Setiap kalimat yang dipakai untuk membangun term t atau membangun sebuah kalimat
F (termasuk F) disebuat subkalimat dari t atau F.
Subterm dan subkalimat sebuah term t atau kalimat F disebut sub ekspressi.
Sebuah subterm sejati, subkalimat sejati atau sub ekspressi sejati adalah dari sebuah ekspressi E adalah
subterm, subkalimat atau sub ekspressi yang berbeda dengan E.
Contoh. Dalam kalimat
F : p(a,x,f(a,x)) and (∃ y)q(g(b,x),y)
subterm dari F adalah :
a, x, f(a,x), b, g(b,x) dan y
subkalimat dari F adalah :
p(a,x,f(a,x)), q(g(b,x),y), (∃ y)q(g(b,x),y), dan F.
Dalam kalimat :
( ∀ x) ((p(x,y) and (∃ y) q(y,x))
Terdapat kejadian x pada scope kuantifier ( ∀ x);
kejadian x ini disebut terikat (bound) oleh kuantifier ( ∀ x).
Kejadian y pada ekpressi p(x,y) tidak didalam scope kuantifier dalam bentuk
( ∀ y) atau (∃ y) sehingga disebut bebas (free). Namun,
kejadian y pada (∃ y) q(y,x)) merupakan terikat (bound).
Kejadian x dan y pada ( ∀ x) dan (∃ y) tidak dikatakan terikat
atau bebas.
Misal x adalah variabel, E adalah ekspressi dalam logika predikat.
Kejadian
x dalam kuantifier (∀ x) dan (∃ x) tidak dikatakan bebas atau terikat.
Kejadian x disebut bound in E jika x berada di dalam scope kuantifier
(∀ x) atau (∃ x) di E. x terikat oleh kuantifier yang terdekat dengannya.
Kejadian x disebut free in E jika x tidak berada di dalam scope kuantifier
(∀ x) atau (∃ x) di E.
Contoh. Dalam kalimat
(∀ x) (( p(x,y) and (∃ x) ( ∀ y) q(y,x))
Kejadian x pada subekspressi terakhir terikat oleh kuantifier (∃ x)
sedangkan kejadian x pada subekspressi pertama terikat oleh kuantigier (∀ x).
| 1. |
Temukan kalimat abstrak dalam bahasa logika predikat
untuk kalimat bahasa manusia berikut ini : a. Untuk semua manusia, tidak ada manusia yang abadi b. Socrates adalah manusia c. Jika socrates adalah manusia dan Untuk semua manusia, tidak ada manusia yang abadi maka socrates tidak abadi. d. Jika semua bilangan prima adalah bilangan ganjil maka beberapa bilangan genap adalah bilangan prima. [Jawaban] |
| 2. |
Temukan subterm, subkalimat dan subekspressi kalimat berikut ini a. (∃ x) (if (p(a,f(g(a,x)),x) and q(x)) then (∀ y) q(y)) b. (∀ x) (∃ y) [if p(y) then p(x)] c if (∀ x,y) p(x,y) then (∀ x) p(x,f(x)) [Jawaban] |
| 3. | Tentukan sifat free atau bound variabel pada tiap kejadian variabel di soal no.2 |
| 1. |
a. (∀ x) (if p(x) then (not q(x))) p merupakan simbol predikat dengan arity 1 merepresentasikan relasi manusia, q merupakan simbol predikat dengan arity 1 merepresentasikan relasi abadi. b. p(a) a adalah simbol konstan yang merepresentasikan socrates, p sama dengan soal 1.a c. if (p(a) and (∀ x) (if p(x) then (not q(x))) ) then (not q(a)) d. if (∀ x) (if prime(x) then ganjil(x)) then (∃ x) (if genap(x) then prime(x)) |
| 2. |
a. (∃ x) (if (p(a,f(g(a,x)),x) and q(x)) then (∀ y) q(y)) Subterms : x,y,a,g(a,x),f(g(a,x)) Subkalimat : q(x),q(y),p(a,f(g(a,x)),x),p(a,f(g(a,x)),x) and q(x), (∀ y) q(y), if (p(a,f(g(a,x)),x) and q(x)) then (∀ y) q(y), dan (∃ x) (if (p(a,f(g(a,x)),x) and q(x)) then (∀ y) q(y)) b. (∀ x) (∃ y) [if p(y) then p(x)] Subterms : x,y Subkalimat : p(y),p(x),if p(y) then p(x),(∃ y) [if p(y) then p(x)] dan (∀ x) (∃ y) [if p(y) then p(x)] c. if (∀ x,y) p(x,y) then (∀ x) p(x,f(x)) Subterms : x,y,f(x) Subkalimat : p(x,y), p(x,f(x)), (∀ x) p(x,f(x)),(∀ x,y) p(x,y) dan if (∀ x,y) p(x,y) then (∀ x) p(x,f(x)) |
| Sebelum Ini | Daftar Isi | Setelah Ini |
| Interpretasi Logika Predikat |